• 标题：揭秘微积分：从基础到高级的解析

标题：揭秘微积分：从基础到高级的解析

常规证明与微积分极限证明

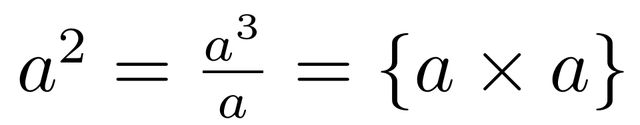
为什么任意非零数的0次方等于1，这是一个基本的数学原理，通过简单的推理，我们可以得出这个结论。

考虑幂的性质，我们知道a的1次方是a，a的2次方是a*a，a的3次方是a*a*a，a的n次方是a*a....*a，n个a相乘。从这里我们可以反推得出：a的2次方 = a的3次方 / a，a的1次方 = a的2次方 / a，那么a的0次方 = a的1次方 / a。

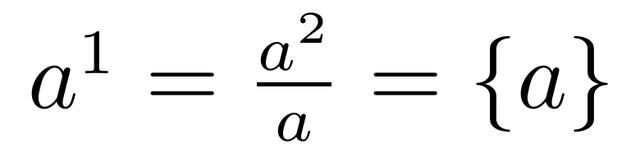
a的0次方等于a的1次方除以a，这是一个基础的数学关系。

进一步，a的-1次方等于a的0次方除以a，这是幂的另一种形式。

微积分的极限证明涉及到当b趋向于无穷时，1/b和-1/b都约等于0，因此a的1/b次方可以看作是a开无穷次方，而a的-1/b次方则是对a开无穷次方的倒数。

夹逼定理是数学中用来判定极限存在的一个重要法则，它告诉我们如果两个数列或函数在某一点附近趋于同一个值，那么中间的数列或函数也必然趋于这个值。

夹逼定理（英文：Squeeze Theorem、Sandwich Theorem，也称两边夹定理、夹逼准则、夹挤定理、迫敛定理、三明治定理，是判定极限存在的两个准则之一。

具体来说，如果数列{Xn},{Yn}及{Zn}满足以下条件：

（1）当n>N0时，其中N0∈N*，有Yn≤Xn≤Zn，

（2）{Yn}、{Zn}有相同的极限a，设-∞<a<+∞

则，数列{Xn}的极限存在，且当 n→+∞，limXn =a。

同样，对于同一连续函数，如果f（0-）≤f（0）≤f（0+）也成立，那么f（0）的极限也存在，且等于1。

通过这些基础知识和高级技巧，我们可以看到微积分并不复杂，只要我们掌握了正确的方法和工具，就可以轻松地解决各种问题。