让我们深入探讨幂函数的倒数！以下是具体的解析：

首先，让我们以三次函数 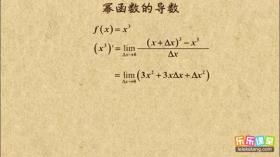f(x) = x^3 为例。我们需要求这个函数的倒数，即 1/x^3 的导数。根据导数的定义，我们需要计算当 x 趋近于 0 时，f(x) + Δf 和 f(x) 的比值。计算后，我们得到导数为 3x^2。可以发现，这里导数的系数 3 恰好等于原函数的指数，导数的指数 2 也等于原函数的指数减去 1。

接下来，我们考虑函数 f(x) = 1/x (x ≠ 0)。我们需要求这个函数的倒数，即 x/(1/x) 的导数。同样地，我们计算当 x 趋近于 0 时，f(x) + Δf 和 f(x) 的比值。计算后，我们得到导数为 -1/x^2。将原函数写作 x^(-1)，我们可以发现，这里倒数的导数 -1 恰好等于原函数的指数，导数的指数 -2 恰好是原函数的指数 -1 再减 1，这与之前的情况一致。

实际上，对于所有幂函数，它们导出的系数等于原函数的指数，导数的指数等于原函数的指数减一，这就是幂函数的求导公式。例如，对于 f(x) = x^5，其导数为 5x^4；对于 f(x) = x^(7/3)，其导数为 (7/3)x^(4/3)。

此外，还有一个特殊的函数 f(x) = c (c 是常数)。这个函数的图像是一条横线，其倒数就是这条直线上某点的切线斜率。无论点在哪里，切线都与直线重合，所以切线斜率当然是 0。因此，常数函数的倒数等于 0。

总结：常数函数的倒数是 0，任意幂函数的倒数都可用求导公式计算，倒数的次数是原函数的指数，倒数的指数是原函数的指数减 1。现在，您是否已经对幂函数的倒数及其求导公式有了更深入的理解？赶紧动手试试吧！